複素数値連続関数 複素平面Cの部分集合Dの中の全ての点zに複素数を対応づけたものを 複素数値関数という。そしてそれはf(z) = u(z)+iv(z)と書き表せる。ここでuが実部でvが虚部である。 複素共役はf*(z) = f(z) = u-ivzが点aで連続であるコトの定義は∀ε>0, ∃δ>0, ∀z: |z-a|<δ ⇒ |f(z)-f(a)|<εまた以下が成り立つ。「f(z)がz=aで連続」⇔「uとvともにz=aで連続」微分可能、正則関数 f(z)が複素微分可能であるとは、lim[|h|→0] {f(z+h)-f(z)}/hが存在すること。実関数の微分と同じように df(z)/dz とかf'(z) とか書く。 今、df(a)/dz = αと値を持ったとすると 十分小さいhに対して常にf(z+h)-f(z)=αh+R(z,h)hとなって、かつh→0の時、R→0となるような R(z,h) が存在する。 この2つは同値。 f(z)がz=aで正則であるとは、f'(z)がその点aで連続であること。 Cの部分集合Dの任意点で正則である時、Dを正則領域という。 べき級数Σ[n=0;∞] anzn (an∈C: 定数)が収束する時、{anzn}がコーシー列になるから、anzn→0 (n→∞の時)のはず。 ならこうも言える。∀ε > 0, ∃M > 0, ∀n > M: |anzn| ≤ εこの右の式をいじってみる。|anzn| ≤ ε ⇔ |z||an|1/n ≤ ε1/n→1(n→∞) ∴|z| lim[n→∞] sup[k≧n] |ak|1/k ≦ 1 ⇔ |z|≦1 / lim[n→∞] sup |an|1/nこの右辺が収束半径である。 10/13 Cauchy-Riemannの関係式 z=x+iy; f(z)=u(x,y)+iv(x,y)f(z)が正則 ⇔ uとvが全微分可能で且つ 「∂u/∂x=∂v/∂y, ∂u/∂x=-∂v/∂y」…CR関係式全微分可能とはu(x+Δx, y+Δy) = u(x,y)+AΔx+BΔy+O(Δの2次以上の項)みたいな形になること。 CR関係式を証明する。 正則であるならば、f'(z)の微分をh=Δx→0で定めても、h=iΔy→0で定めても その値は一致するはずである。確かめてみよう。lim[h→0] {f(x+Δx,y)-f(x,y)}/Δx = lim {u(x+Δx,y)-u(x,y)}/Δx + lim{iv(x+Δx,y)-iv(x,y)}/Δx = ∂u/∂x + i∂v/∂x lim[h→0] {f(x,y+Δy)-f(x,y)}/(iΔy) = lim {u(x,y+Δy)-u(x,y)}/(iΔy) + lim{iv(x,y+Δy)-iv(x,y)}/(iΔy) = (1/i)∂u/∂y + ∂v/∂yこの二つの値は一致するはず。つまり実部と虚部はそれぞれ一致する。 比較すると∂u/∂x = ∂v/∂y ∂v/∂x = -∂u/∂yを得る。 別な証明の仕方として、f(z)をxとyの合成関数と看做して微分してみる という説明もあったけどよく分かんなかった。厳密な証明ではなかったし。 例として、f(z)=z2、f(z)=log(z) などで試してみよ。 調和関数 さっき続き。 CR関係式を用いると∂2u/∂x2+∂2u/∂y2 = ∂/∂x(∂v/∂y)+∂/∂y(-∂v/∂x) = 0同様にして∂2v/∂x2+∂2v/∂y2 = 0を得る。 二次元ラプラシアンを用いてΔu=0, Δv=0と書けてこれをLaplace方程式という。 CR関係式を用いれば、u,vの一方からもう一方は定まる。 微分の形だから積分定数の項だけ付くだけど。 例として u=3x2y-y3 とすると∂u/∂x = 6xy ∴∂v/∂y = 6xy ∴v=3xy2+A(x) -∂u/∂y = -3x2+3y2 ∴∂v/∂x = -3x2+3y2さっきのvをコレに代入すると3y2+dA/dx = -3x2+3y2 ∴A(x)=-x3+C よって v=3xy2-x3+Cよってこのuが登場するf(z)はf(z)=u+iv = 3x2y-y3+i(3xy2-x3+C)ジッと睨むと= -i(x+iy)3+iA = -i(z3+A)でしたとさ。 正則とはなんだったのか 正則ではない例としてf(z) = Re(z) = x f(z) = z = x-iyzだけの(zなどを含まない)普通の(zn,log(z),cos(z)..,ez..)関数なら まあ大体正則だ。 でも 1/(z-a) とか明らかな不連続点があるものはその点で連続ではない。 複素積分 線積分と同じことをする。 f(z)を[z0,z1]で積分する時、複素平面上でzstartからzendを結ぶ方向付きの 経路を考えて、それによって積分する。経路によって積分値は違うかもしれない。 経路を微小区間に分ける。 不取敢、n分割する。zstart=z0, z1 .. zn=zend Δzi = zi-zi-1あとでn→∞にしよう。経路(path)をCとして ∫Cf(z)dz = lim[n→∞] Σ[i=1;n] f(zi)Δziこれが収束値を持つなら、それを積分値としよう。 具体的にはどう計算するか。 経路Cを、例えばパラメータtを用いて z=z(t) と表す。 そしたら Δzi=dz(t)/dtΔt とすればよい。 註) 経路Cが実軸上なら実数の積分と同じ 虚軸上ならC:z(y)=iy と書けて∫Cf(z)dz=∫y0y1 f(z=iy)・(idy)例。 f(z)=z を 経路C:z(t:0→2π)=r・exp(it) で積分する∫C f(z)dz=∫02π r・exp(it)・ir・exp(it)dt = ir2∫exp(2it)dt = ir2/(2i) [exp(2it)]02π = 0f(z)=zは全空間で正則である。次は正則では無い例。 f(z)=1/z を C: z(t:0→π)=r・exp(it) で積分する。∫C f(z)dz = ∫0π 1/(r・exp(it))ir・exp(it)dt = i∫0πdt = iπ今度は経路C': z(t:0→-π)=r・exp(it) で積分するとI = -iπとなるよ 経路の最初の点と最後の点が一致する時、∫C dzを∮C dzと書いて明示する。 もうちょっと例。 C:z(t:0→2π)=r・exp(it) という経路で∮dz/z = ∫02π {ir・exp(it)}/{r・exp(it)}dt = 2πi ∫1/zn・dz (n≧2) = ∫02π {ir・exp(it)}/{r・exp(it)}n dt = 0複素積分の性質 線積分と同じ。∫C1+C2 = ∫C1+∫C2 経路Cの逆向きを -C と表すと ∫C = -∫-CThm. 関数列{fn(z)}がf(z)に一様収束する時、∫C fn(z)dz = ∫C f(z)dzである。ε-δで説明しようとすればできるけどしないよ。 これの系として、lim[N→∞] ∫C Σ[n=0;N] cnzndz = ∫C lim[N→∞] Σ[n=0;N] cnzndzすなわち、limと∫は交換が可能である。項別積分できるのだ。 Cauchyの積分定理 f(z)が単連結領域(穴が無い)で正則ならば、その領域内の任意の閉曲線Cに対して∮C f(z)dz=0である。 f(z)=z, cos(z), ez...etc は全空間で正則である。 z1/2はz=x(x>0)で正則ではない(リーマン面)。 だからz=r・exp(it)という経路はダメ。 この積分定理を簡単に証明する。∮C f(z)dz = ∮C (u+iv)(dz+idy) = ∮C (udx-vdy+ivdx+iudy) = ∮C (udx-vdy) + i∮C (vdx+udy)ストークスの定理(グリーンの定理)を用いると、 閉曲線上の積分が面積上の積分になる。例えば ∮(udx - vdy) は A(x,y) = (u, -v) という関数の周回積分である。 そしてストークスによると ∫ rot(A) dS と一致する。I = ∬(-∂v/∂x-∂u/∂y)dS + i∬(∂u/∂x-∂v/∂y)dSCR関係式をぶち込むとI = 0正則な領域の中なら、「z:z0→z1」という積分の値は経路によらない。 z0→z1の経路としてC1とC2という二つを考えた時、 C1-C2という経路は閉曲線であり、∫C1-C2 f(z)dz = 0 ⇔ ∫C1 f(z)dz = ∫C2 f(z)dzとなるから。 閉曲線に囲まれた領域の中に特異点が一つあったとする。 そうするとコーシーの定理が使えない。ならば避けて閉曲線を作れば良い。 一応、正則な領域のみを通る閉曲線である。
∫A+∫B+∫C+∫D = 0∫A'+∫B'+∫C'+∫D' = 0BとB'、DとD'は一致させてやってもいい。ただし逆向きだからB=-B', D=-D'とする。そして先の二つの経路を足してやると∫A+∫A'+∫C+∫C' = 0を得る。 A+A'は一つの閉曲線になっていて、それを改めてAとする。 C+C'もまた改めて閉曲線Cとする。∫A+∫C = 0AとCは逆向きである。大体数学では反時計回り、内回り線を正と するから、-AをA'とすると∫A' = ∫C閉曲線は、正則な領域内ならば(曲線の上に特異点がなければ)、 伸び縮みさせても積分値は変わらない。 ∮dz/(z-a) を考える。特異点はz=aの一つ。 その周りの経路で積分するなら、どんな経路でもいいんだから 計算しやすいのを選ぼう。z(t)=a+r・exp(it)これで積分するとI = ∫02π {ir・exp(it)}/{r・exp(it)}dt = 2πiが求まる。
10/20 コーシーの積分公式 単連結領域Dでf(z)が正則であるとき、Dの中の閉じた経路Cでf(a) = (1/2/π/i) ∮C f(z)/(z-a)dz ただし、aは(C)の内点が成り立つ。 証明。コーシーの積分定理を使う。 点aのすごく近傍の閉じた経路γを考える。 例えばγ: z(θ:0→2π)=a+r・exp(iθ)とする。 このrをすごく小さくする。それはつまり、次の式のδである。∀ε > 0: ∃δ > 0: ∀|z-a| < δ: |f(z)-f(a)| < εこのδを使ってγ: z(θ:0→2π) = a + δ・exp(iθ)とする。 コーシーの積分定理より、 f(z)/(z-a)の一周積分はCの経路でもγの経路でも 同じ方向なら同じ値である。z=a が唯一の特異点であり、経路で囲われた領域 の中にあるから積分値は0ではない∮γ f(z)/(z-a) dz=∮ [(f(z)-f(a)) + f(a)]/(z-a) dz = ∮ [f(z)-f(a)]/(z-a) dz + ∮ f(a)/(z-a) dz∮ f(a)/(z-a) dzこの値は実際に求められる。つまり、f(a)は定数であるのと、 z=a+δexp(iθ)を代入すればdθの∮に書き換えられて I=2πif(a) これを代入して式変形してやると|(1/2/π/i) ∮γ f(z)/(z-a)dz-f(a)| = (1/2/π/i)|∮γ [f(z)-f(a)]/(z-a)dz|右辺はεを使って抑えることができる。つまり、|∮ [f(z)-f(a)]/(z-a) dz| < ∮ |[f(z)-f(a)]/(z-a)|dz < ∮ |ε/(z-a)|dz = 2πεi今ε→+0とすれば、右辺は0に収束して、(1/2/π/i) ∮C f(z)/(z-a) dz = f(a)を得る。 ● ∮C dz/z/(z+2) ;C:z(t:0→2π)=exp(it)f(z)=1/(z+2)とする。特異点はz=-2のみであり、これは(C)の外にある。 コーシーの積分公式より、f(a) = ∮C f(z)/(z-a) dz = ∮C 1/z/(z-a) dza=0 とすると求める答えがf(0)だとわかる。// f(z)=1/z とすると、特異点が(C)の中にあって公式が使えない。f(a) = 1/2/π/i ∮C f(z)/(z-a) dzであった。z=aの近傍点z=a+hでは、f(a+h) = 1/2/π/i ∮C f(z)/(z-a-h) dzである。微分の定義から、f'(a)が求められそうだ。f(a+h)-f(a) = 1/2/π/i ∮ f(z)[1/(z-a) - 1/(z-a-h)]dz = 1/2/π/i ∮ f(z) h/(z-a-h)/(z-a) dz両辺をhで割って、h→0とすればf'(a) = 1/2/π/i ∮C f(z)/(z-a)2 dzと表せる。これを再帰的に使うことによってn次微分が求められてf(n) = n!/2/π/i ∮C f(z)/(z-a)n+1 dz nは0を含む自然数「f(z)が正則」⇔「何回でも微分できる」 Liouvilleの定理。 f(z)が有界な整関数である、とは、∃M>0, ∀z: |f(z)|<Mとなること。つまり無限に発散しないことであり、正則であるとも言える。 そして今f(z)がそうあるとき、f'(z) = 1/2/π/i ∮C f(ζ)/(ζ-z)2 dζとなるのはコーシーの積分公式。 Cをz(t:0→2π)=Rexp(it) とする。|f(ζ)/(ζ-z)2| < M/(|ζ|-|z|)2 //分母は三角不等式 = M/(R-|z|)2これはR→+∞ で0に収束するから1/2/π/i ∮C M/(R-|z|)2もR→+∞で0に収束する。だって積分範囲は有限だから0が発散することはない。 よってf'(z) = 0となる。zは(C)の任意の内点だから、f(z)は定数である。 これより、C∩{±∞} で正則な関数f(z)は定数であることになる。 テイラー展開f(z) = 1/2/π/i ∮C f(ζ)/(ζ-z) dζであった。 経路Cの中心をz0とする。中心であるとはつまり、 経路C上のζ、(C)の内点zにたいして|ζ-z0| > |z-z0|がいつも成り立つということ。 そしてそのz0を用いて1/(ζ-z) = 1/[(ζ-z0) + (z0-z)] = 1/[(ζ-z0) - (z-z0)] = 1/(ζ-z0) [1-(z-z0)/(ζ-z0)]-1今、|(z-z0)/(ζ-z0)|<1 である。 その時、[1-k]-1 = 1+k+k2+…の右辺が収束するのを参考にして1/(ζ-z) = 1/(ζ-z0) [1+[(z-z0)/(ζ-z0)]+[(z-z0)/(ζ-z0)]2+…] = Σ[n=0;∞] (z-z0)n/(ζ-z0)n+1となって右辺は収束する。 収束するんだから積分と積和は入れ替えてもいい。 つまり、最初の式に代入して、f(z) = 1/2/π/i ∮C f(ζ) 1/(ζ-z) dζ = 1/2/π/i Σ[n=0;∞] ∮C (z-z0)n/(ζ-z0)n+1 f(ζ) dζそしてcn = 1/2/π/i ∮C f(ζ)/(ζ-z0)n+1 dζとおけばf(z) = Σ[n=0;∞] cn (z-z0)nと級数で表せて、まさしくテイラー級数である。 さっきのf(n)の形とcnを見比べるとcn = (1/n!)f(n)(z0)となっていて、完全に実関数のテイラー展開と同じだ。 Laurent展開 正則ならテイラー展開をすればよかった。 じゃあ特異点を持つ場合はどうしようか。 特異点aがあってそれを中心とする経路Cでf(z)を積分するとき、 コーシーの積分公式は使えない。 Cの途中で点aに向かってaの周りを小さく回って、そして もとのCに戻ればいい。最初のCをC外として、aを中心に(小さく)回る のをC内としよう。C内はC外とは逆方向になっちゃうので C外と同じ向きをC内とする。積分経路は-C内である。 C外-C内は一応正則領域にあるからコーシーの積分公式は使えるのだ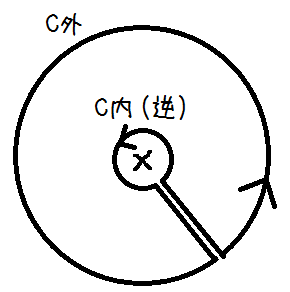
f(z) = 1/2/π/i ∮C外 f(ζ)/(ζ-z) dζ - ∮C内 f(ζ)/(ζ-z) dζ//被積分関数の特異点はζ=aおよびζ=zの2つだから値が同じというコーシーの積分定理は使えない C外では |ζ-a|>|z-a| が成り立っていて、これは先ほどと全く同じでΣ[n=0;∞] cn(z-a)nとなるだろう。 問題はC内であり、ここでは|ζ-a|<|z-a|である。式の変形を次のように工夫する必要がある。1/(ζ-z) = -1/[(z-a) - (ζ-a)] = -1/(z-a) [1-(ζ-a)/(z-a)]-1 = -1/(z-a) Σ[n=0;∞] [(ζ-a)/(z-a)]n = -Σ[n=0;∞] (ζ-a)n/(z-a)n+1故に、-1/2/π/i ∮C内 f(ζ)/(ζ-z) dζ = +1/2/π/i Σ[n=0;∞] 1/(z-a)n+1∮ f(ζ)(ζ-a)n dζn+1=-m と書き換えるとΣ[m=-1;-∞] (z-a)m ∮ f(ζ)(ζ-a)-m-1 dζcm = 1/2/π/i ∮C内 f(ζ)(ζ-a)-(m+1)dζ としてやると これの被積分関数の特異点はただζ=aだからコーシーの積分定理より、 cm = 1/2/π/i ∮C外 f(ζ)(ζ-a)-(m+1)dζ としても同じ。 そして-1/2/π/i ∮C内f(ζ)/(ζ-z)dζ = Σ[n=-1;-∞] cn(z-a)nC外のと合わせてやればf(z) = Σ[n=-∞;∞] cn(z-a)n ;cn = 1/2/π/i ∮C外 f(ζ)/(ζ-a)n+1 dζとなった。これをローレンツ展開という。 留数 コーシーの積分公式は、f(z)及びf(z)のn次微分ををfの一周積分で表すから ぐるぐるまわって面白い。 さてローレンツ展開での係数{c_n}について、∃m ≥ 1: c_{-m} ≠ 0, c_{-m-1} = c_{-m-2} = .. = 0の時、c_{-m}を、関数f(z)の特異点z=aに就いての、m位の留数という。 Res_a(f)とか書いて表す。 大抵の場合、留数というのは1位か2位くらいのものなのだ。 さっきのコーシーの積分公式で f(z)が(C)に特異点を持たなければf(a) = 1/2/π/i ∮C f(z)/(z-a)dzであった。f(z)/(z-a)を改めてf(z)と置くことにする。 f(z)の特異点は(C)にはz=aの一点である。(z-a)f(z)|z=a = 1/2/π/i ∮C f(z) dzこの右辺は、f(z)をローレンツ展開した時の1位の留数c-1である。 個人的にややこしいので何度でもまとめ直して書こう。経路Cがあって、f(z)は(C)に一点z=aという特異点を持つとすると ∮C f(z) dz = 2πi ∮C f(z)/(z-a) dz = 2πi c-1問題はc-1をどうやって計算するかである。 大抵は lim[z→a] (z-a)f(z) で求まるのである。 次の「孤立特異点」の章でちゃんと書く。 それよりも特異点の周りのコーシーの公式をローラン展開で逆に導ける。 (もともとローラン展開はコーシーの公式から導かれたのだけど) (C)に特異点z=aを持つf(z)についてf(z) = Σ[n=-∞;∞] cn(z-a)n両辺をCで一周積分しよう。 右辺は項別積分でいいだろう。一様収束することを期待して。∮C (z-a)n = 0 (when n is not -1 2πi (when n is -1これはC: z(t)=a+exp(it) などして求めれば良い。 これを代入すると∮C f(z)dz = 2πi・c-1とさっきと同じ結果が出る。
10/27 孤立特異点 - ローラン展開による特異点の分類 特異点がその積分路内に一つだけある時、その特異点を次のように三つに 分類できる。 f(z)をローラン展開したとする。つまり、(z-a)nの係数の列{cn}を求める。 i) n<0でいつもcn=0ならローラン展開はテイラー展開になる。 だからf(z)は正則である。 逆に正則なf(z)についてcn = ∮C f(z)(z-a)-n-1dzn<0ならf(z)(z-a)-n-1も正則で、正則関数の一周積分だからcn = 0となる。(逆を示しただけだけどね) u) ∃k>0, ∀n<-k: cn = 0, c-k ≠ 0 である時、 ローレンツ展開はf(z) = Σ[n=-k;∞] cn(z-a)nと書けて特異点を「k位の極 (k-th order pole)」という。 w) (u)のkが∞の時、つまりc-∞≠0の時、特異点を 真性特異点(essential sigularity)という。 例えば「f(z)=exp(1/z)」は z=0 が真性特異点である。 留数定理 特異点z=aの周りでローラン展開した関数をその特異点z=aの周りで 一周積分する。∮C f(z)dz = 2πi・c-1// これさっき自分で導いたよ。。 問題はやはり、c-1の求め方である。 1位の極の時、f(z) = c-1(z-a)-1 + c0 + c1(z-a) + …とローラン展開される。 両辺を(z-a)倍してz→aとすれば(z-a)の非負整数が右肩にのってる 項が掛かっているのはゼロになって、結果的に(z-a)f(z)|z→a = c-1として導くコトができる。 基本的にはこういう考え方。 2位の極である時、f(z) = c-2(z-a)-2 + c-1(z-a)-1 + c0 + …(z-a)倍しただけだとc-2が残るから、両辺を(z-a)2倍して(z-a)2f(z) = c-2 + c-1(z-a) + c0(z-a)2 + …両辺zで微分して(d/dz)(z-a)2f(z) = c-1 + 2c0(z-a) + …z→aすれば右辺はc-1になる。 一般に、 k位の極の周りでローラン展開したら留数はc-1 = lim[z→a] 1/(k-1)! (d/dz)k-1[(z-a)kf(z)]である。 /* 2位の極なのに1位の極だと思って留数c-1を求めようとするとc-2/(z-a)+c-1→c-2・∞と発散してしまう。 だから、1位と信じて留数求めて、結果が±∞だったらじゃあ2位だと 思ってそれで留数求めて、それでも発散したら3位だと思って たぶんそろそろ真性特異点なのを疑えばいいんじゃないかと思います。 */ 定積分の応用例 実関数の定積分。 そのままでは解きにくい、あるいは全く解けそうにないが複素平面上で 積分すると解けることがある。f(x)の積分からg(z)の積分に移すのである。 fからどのようなgにしたらよいか。また積分経路も考えなければいけない。 経路Cは実軸上のC1とその他のC2からできているとして、∮C g(z) dz = ∮C1 g(z) dz + ∮C2 g(z) dzとなるが、∮C1 g(z) dz = ∫ f(x) dx ∮C2 g(z) dz →0 とかとなるようなCを考えるのである。 ●∫-∞∞dx/(x2+1) = π これくらいならx=tan(t)と置換しても解けるけど,複素平面上での積分を考えよう。f(z)=1/(z2+1)とするとf(z)を実軸上で積分するなら1/(x2+1)の積分と一致するだろう。(基本は、z=x+iyとしてy=0であること) 次のような経路Cを考える。 C1: z(t:0→π)=R・exp(it) と C2: z(x:-R→R)=x の和 このCの一周積分を考えて、R→+∞にする。 f(z)の特異点はz=i,-iの二つで(C)の中にあるのはz=iだけ。∮C f(z)dz = 2πi(z-i)f(z)|z=a = 2πi/(x+i)|z=i = 2πi/(2i) = π ∮C1f(z)dz = ∮C11/(z2+1)dz = ∫0π 1/(R2exp(2it)+1) (iRexp(it)dt) //z(r,t)=rexp(it) → ∫0dt (R→∞の時) = 0 (積分範囲が有限なので) ∴∫C2f(z)dz→π(R→∞の時) ∴∫-∞∞1/(x2+1)dx=π●∫-∞∞cos(kx)/(x2+a2)dx (kは自然数) = exp(-ka)/(2ia) cos(kx)がexp(iz)の実軸上だと見ると f(z) = exp(iz)/(z2+a2) とすると、特異点はz=ia,-iaの二つで実軸上[-∞,∞]の積分が求めたい 積分と一致する。 経路C: C1+C2 C1: z(t:0→2π) = R・exp(it) のR→∞ C2: z(x:-∞→∞) = x で積分しよう。 ∮C f(z)dz = 2πi(f(z)(z-ia))|z=ia = π/a exp(-ka) ∫C1 f(z) dz = ∫0π exp(ikReit)/(R2e2it+a2) dt で、大抵無限に飛ばす予定のRを半径にする円周上の 積分値というのは0になるコトを期待している。 積分範囲は有限だから、被積分関数がR→∞で0に収束すればいい。 exp(ikReit)/(R2e2it+a2) の分母はR→∞で明らかにゼロになる。 分子は exp(ikReit) = exp(ikR(x+iy)) //(eit=x+iy) = eikRx・e-kRy eikRxはeの虚数乗だから絶対値が1。つまり発散もしない。 e-kRyはeのマイナス乗である(0≤t≤πであるからy≥0) のでR→∞で0に収束する。 よって∫C2 f(z)dz→0 ∫C f(z)dz = ∫C1f(z)dz+∫C2f(z)dzより、 求めたい積分値は π/a exp(-ka) である。 ●∫02πdt/(a+cos(t)) = 2π/√(a2-1) ●∫0∞ sin(x)/x dx = π/2 f(z)=exp(iz)/z を経路C=C1+C2+C3+C4で積分する。 z=0が特異点であり、これを避ける積分範囲を考える。 C1: z(t:π→0)=r・exp(it) のr→+0 C2: z(x:+0→+∞)=x C3: z(t:0→π)=R・exp(it) のR→∞ C4: z(x:-∞→-0)=x C3の積分値は0に収束する C1の積分値はそれっぽいのが出る。 C2及びC4の積分値はexp(iz)=exp(-y)exp(ix)=exp(-y)[cos(x)+icos(x)] として実部と虚部それぞれ分けて積分を考える。 偶関数であるか奇関数であるか。 実部は奇関数であるのでC2とC4を足すと0になるのだ。 代数の基本定理 定数でない多項式f(x)について、複素平面上の方程式「f(z)=0」は必ず解を持つ。 これを複素解析によって証明できる。 いつもf(z)≠0なら 1/f(z) は正則であることになる。 テイラー展開によって1/f(z) = Σ[n=0;∞] cnznと表せる。 f(z)は多項式だからz→∞とした時、f(z)は発散する。即ち1/f(z)→0 (z→∞)である。 そしたらΣ[n=0;∞] cnzn→0とならなければいけない。 c∞≠0だとz→∞で発散してしまう。だから無限級数ではない。 大きい方から再帰的にして結局cn=0となる。代入するとf(z) ≡ 0という定数になってしまう。多項式であることに矛盾する。 よって1/f(z)は正則ではない。 解析接続 (analytic continuation) 正則な領域内で、z~aの周りでf(z)をテイラー展開する。領域の外に 特異点z=bがあるとすると、先のテイラー展開の収束半径は|a-b|である。 例えば、f(z) = (1-z)-1 はz~0でf(z) = Σ[n=0;∞] znであるが、z=1が特異点であるので |1-0|=1 が収束半径である。 |z-0|≤1 の時だけ先の級数は収束する。 z=0を中心に半径1の円の中である。円周は含まない。 では次は z~iの周りでテイラー展開してみる。 (1-z)-1 = (1-i)-1・(1-[(z-i)/(1-i)])-1 と変形すればわかりやすくてf(z) = (1-i)-1 Σ[n=0;∞] [(z-i)/(1-i)]nとテイラー級数で表せる。 今度の収束半径は |1-i|=√2 である。 z=iを中心に半径√2 の円の中である。円周は含まない。 |z|<1かつ|z-i|<√2の範囲があるが、この時、二つのテイラー級数 は同じ値に定める。本当だよ?これを一致の定理という。物理数学は そんな細かい証明は必要ないのだ。 さて2つ目のテイラー級数の収束領域は、一つ目のそれと少しズレている。 そして一つ目よりも大きい。うまくコレを繰り返すコトによって特異点だけ を除いた全ての範囲でテイラー展開ができる。この操作を解析接続という。 f(z)は実軸上でexp(z)と一致するとする。f(z)が全域で正則であるとf(z) は全域でexp(z)と一致するだろうか。先の一致の定理を用いると一致する。 同様に実軸上でcos(z)となる正則関数はcos(z)に限る。 Cauchy-Riemannの関係式から「∂u/∂x=∂v/∂y」(久々だ)を用いれば 実軸上から全域に接続解析することが出来る。 ● f(z) = exp(-z2) これは全域で正則。C1: z(x:0→R) = x C2: z(t:0→π/4) = R・exp(it) C3: z(r:R→0) = r・exp(iπ/4) C = lim[R→∞] (C1+C2+C3)f(z)をCに沿って一周積分する。 ∫C2 f(z)dzはR→∞で0に収束するだろう。めんどいのでパス ∫C1 f(z) dz → ∫0∞ exp(-x2) dx これはガウス積分で√π/2である。一応求める過程を書くとI = ∫0∞ exp(-x2) dx I2 = ∫∫0∞ exp(-x2-y2) dxdy ここで (x,y)を(r,t)に変換する。つまり x = r・cos(t) y = r・sin(t) dxdy = rdrdt を代入すると I2 = ∫0π/2∫0∞ r・exp(-r2) drdt = ∫0π/2 (1/2) dt = π/4 exp(-x2) > 0 なので I > 0 で、 I = √π/2∫C3 exp(-z2) dz = -∫0R exp(-r2exp(2i・π/4)) (eπ/4・idr) → -∫0∞ exp(-ir2)(1/√2+i/√2)dr (∵exp(it)=cos(t)+i・sin(t)を使った) = -(1/sqrt(2)+i/sqrt(2)) ∫ [cos(r2)-i・sin(r2)] drI1 = ∫-∞∞ cos(x2) dx I2 = ∫-∞∞ sin(x2) dxと置くと ∫C3 exp(-z2) dz = -(1/sqrt(2)+i/sqrt(2))(I1-iI2) = -1/sqrt(2)(I1+I2) -i/sqrt(2)(I1-I2) と求まる。 f(z)は正則だったから一周積分はゼロ。つまり∫C1+∫C2+∫C3 = 0 全部に代入して実部と虚部を比較するとI1 = I2= (1/2)sqrt(π/2)となる。 逆に「∫-∞∞ cos(x2) dx」から「exp(-z2)」は思いつかないよねえ。。 δ関数 実軸上では正則なf(z)について、 f(z)/(z-a) を、次のような経路で一周積分する。 特異点 z=a を避けるようにC1: z(x: a+ε → +R) = x C2: z(t:0→π) = R・exp(it) C3: z(x: -R→a-ε) = x C4: z(t:π→0) = a+ε・exp(it)Rは∞に飛ばして、εは+0に飛ばす。 C1+C2+C3+C4で一周積分する。 ∫C2 f(z)/(z-a) dz はきっとゼロになるだろう。 ∫C4 f(z)/(z-a) dz はちゃんと求まってI = ∫π0 f(a+εeit)i dt → -iπf(a) (ε→+0の時)特異点をεだけ避けて、そうしてε→+0とする、をPと表し 主値(principal)と呼ぶ。∫C1+C3 f(z)/(z-a) dz = [∫0a-εdz + ∫a+ε∞ dz] f(x)/(x-a) → P∫-∞∞ f(x)/(x-a) dxと使う。「P∫」を「主値積分」と呼ぶ。∮C f(z)/(z-a) dz = P∫-∞∞ f(z)/(z-a) dz - iπf(a)同じ周回積分を違う経路から近づいて、計算する。C'1: z(x:-R→R) = x+iδ C'2: z(t:0→π) = R・exp(it) C' = lim[R→∞, δ→+0] C'1+C'2に沿って積分する。∫C'2 f(z)/(z-a) dz はきっとゼロに収束して ∫C'1 f(z)/(z-a) dz = ∫-∞∞ f(x+iδ)/(x-a+iδ) dx ~ ∫-∞∞ f(x)/(x-a+iδ) dx前のとあわせてlim[δ→+0] ∫-∞∞ f(x)/(x-a+iδ) dx = P∫-∞∞ f(x)/(x-a) dx - iπf(a)が得られる。 次のようなδ(x)関数を考えよう。左辺のデルタは十分ゼロの定数で右辺がδ関数である。lim[δ→+0] 1/(x-a+iδ) = P/(x-a) - iπδ(x-a)そしてこれがδ(x)の定義である。 このδ(x)の意義とは、両辺にf(x)を掛けて積分した時、∫-∞∞ f(x)δ(x-a)dx = f(a)となる。なるように定義したのである。 さて、∮C f(z)/(z-a) dz = P∫-∞∞ f(z)/(z-a) dz - iπf(a)f(z)が複素平面の上半面で正則なら、∮C f(z)/(z-a) dz = 0であり、P∫-∞∞ f(z)/(z-a) dz = iπf(a)この両辺の実部、虚部を取るとP∫-∞∞ Re[f(z)]/(z-a) dz = -πIm[f(a)] P∫-∞∞ Im[f(z)]/(z-a) dz = πRe[f(a)]という関係式が得られ、これを「Kramers-Krönigの関係式」という。 f(z)の実部が分かっていればこの関係式から虚部も求まり、 逆に虚部から実部を求めることも可能であり、趣深い。 --- 11/10g(ω) = b / (ω - E/ℏ + iγ) ;γ>0のフーリエ変換を考える。f(t) = ∫-∞∞ e-iωt g(ω) dω = ∫-∞∞ b/(ω-E/ℏ+iγ) e-iωt dω複素平面上の積分路を考える。C: lim[R→∞]{ z(x:-R→R)=x } + { z(t:0→π)=R・exp(it) } C': lim[R→∞]{ z(x:R→-R)=x } + { z(t:-π→0)=R・exp(it) }// C'の向きに注意 半円孤上での積分値はゼロに収束することを期待している。 Cの円弧上での積分はexp(-iωt) = exp(-iRe(ωt))・exp(Im(ωt))このIm(ωt)が発散しなければよい。CではIm(ω)>0だからt<0の時、 これはゼロに収束する。ではt>0の時はどうするか。C'で積分すればよい。 では積分しよう。 被積分関数の極はω=E/ℏ-iγ であり、複素平面の下面にある。 だからCで積分するとゼロ。 向きを考えて -C' で積分するとf(t) = -2iπ c-1 //留数定理 c-1 = (ω-E/ℏ+iγ)g(ω)|ω=E/ℏ-iγ = b・exp(-iEt/ℏ-γt)以上からf(t) = 0 when t<0 -2πibeiEt/ℏ - γt when t>0t=+0の時、f(t) = -2πibであり、exp(-γt)は減衰、exp(-iEt/ℏ)は振動を 表すのでf(t)は減衰振動である。 「t<0」→「t>0」で振動が始まるという因果律を表す。 もし極が上面にあったら、これが逆になるので因果律が破れる。 t=0 では、上では求められていないが、t=0を代入してから積分すると f(0) = ∫b/(ω-α) dω = P∫b/(ω-α) dω - iπ∫bδ(ω)dω = 0 -iπb // P∫b/ω dωは反比例グラフを連続なトコだけ積分 故にf(0) = [f(-0)+f(+0)]/2 となる。 フーリエ変換だから当たり前だね。 γ=δ→+0 とすると、振動の寿命が延びる。 さらにE=0とするとf(t) = ∫-∞∞ be-iωt/(ω+iδ)dω = -2iπb (when t>0) 0 (when t<0)Heviside関数 θ(x) = 1 (when x>0) 1/2 (when x=0) 0 (when x<0)を用いる。 先の γ=δ, E=0 の f(t) は、f(t) = -2πibθ(t)と書ける。f'(t) = -2πibθ'(t) = -2πibδ(t) (d/dt)f(t) = (d/dt)[∫b/(ω+iδ)exp(-iωt)dω] = ∫-iωb/(ω+iδ) exp(-iωt) dω → -ib・∫exp(-iωt) dω故に 2πδ(t) = ∫-∞∞ exp(-iωt) dω 右辺は1のフーリエ変換を意味する。 t≠0 なら右辺がゼロなので右辺の積分値もゼロである。 t=0 な両辺無限大になる。 等角写像(conformal mapping) 複素平面上で定義されたω = f(z)がz=z0で、正則かつf'(z0)≠0なら、z~z0の周りで 一対一対応でしかも角度を保存する等角写像である。 角度を保存するとは即ち、 z0,z1,z2がfによってω0,ω1,ω2に写される時に∠z1z0z2 = ∠ω1ω0ω2である。但し、z1,z2はz0の近傍。 等角であることを示す。θ = ∠Xz0z1 - ∠Xz0z2 = arg(z1-z0) - arg(z2-z0) = arg( (z1-z0)/(z2-z0) ) 一方写った方は θ' = arg( (ω1-ω0)/(ω2-ω0) ) f'(z0) = lim[z1→z0] (f(z1)-f(z0))/(z1-z0) = lim (ω1-ω0)/(z1-z0) = α 一方、微分は正則なら近づき方に関係無いハズで f'(z0) = lim[z2→z0] (f(z2)-f(z0))/(z2-z0) = lim (ω2-ω0)/(z2-z0) = α α≠0で、これを代入すれば θ=θ'例として、f(z)=z2 によって x=a がどう写るか考える。f(z) = (x2-y2) + i(2xy) u = x2 - y2 v = 2xy写る先をuv空間とすればよい。 x=aを代入してu = a2 - y2 (-∞<y<∞) v = 2ay (-∞<y<∞)yを消すようにすればv2 = -4a2u+4a4という放物線に写ることが分かる。 次にy=bはどう写るか。u=x2-b2 v=2bx -∞<x<∞に写る。 xを消せば、4b2u + 4b4 = v2という放物線に映るが、これはさっきの放物線と直交するはずである。 ちなみに、x=aとy=bが直交するのはいいとして、交点は一つであるが、 写った先の二つの放物線は交点を二つ持つ。そういうものである。次の例。 f(z) = exp(z) = ex cos(y) + iex sin(y) これはx=aを (u=ea cos(y), v=ea sin(y)) に写す。半径eaの円周上である。 y=bを (u=ex cos(b), v=ex sin(b)) に写す。ex>0に注意するとこれは原点から伸びる半直線である。 Potential問題への応用 さっきの最後の例は原点に荷電を置いた時の等ポテンシャル面、電気力線 と見ることができる。複素平面上であるので、二次元に限るが、ポテンシャル 問題に応用することができる。 等ポテンシャル線、電気力線は直交する。その垂直を保つように写像fに よって直線に写したい。等ポテンシャルを「u=α」、電気力線を「v=β」に 写せたら分かりやくて良いだろう。 角度を保存する写像は正則だからCauchy-Riemann関係を満たし、さらに 調和関数になっている。つまりΔu=0。uはポテンシャルである。
/* 静電場Eはdiv E = ρ、E = -∇u を満たす。 故にΔu = -ρ (二次元の場合) ρ=0ならばΔu=0 */先の最後の例の逆写像を考えたいからf(z) = log(z)を考える。f(z) = log(reit) = log(r)+it (r2=x2+y2, t=tan-1(y/x)) u = log(r) = (1/2)log(x2+y2) v = t = tan-1(y/x)原点に一つ電荷を置いた場合を考えて 等ポテンシャル線: x2+y2-r2 = 0 はfによってどこに写るか。u = r(一定), -π < v < π電気力線: y = tan(t)・x はfによって-∞ < u < ∞, v = t(一定)x=aに正電荷とx=-aに負電荷を置いた場合はf(z) = log(z-a)-log(z+a)とすればよい。 註) 二次元ポテンシャルではu(r) = log(r)となるが 三次元ではu=1/rとなるはず(係数無視)。 三次元においてz軸に線電荷を置いた場合と考えれば二次元のそれとなる。 またこの原因は、三次元は(1/r2)を積分から求められるのを、 二次元では(1/r)を積分した形だからである。 次の例。 xy平面で、x<0とy<0の領域を導体、その残り(第一象限)を真空とする。 導体の表面に一様な正電荷を帯電させる。この場合の等ポテンシャル面と 電気力線がどうなるか解いてみよう。 先の場合と同様に、どこかから偶然見つけたようにf(z)を持ってくる必要が ある。大事なのは、自明な曲線について、それが然るべき曲線に写される ようなf(z)を自分で考えることである。 今の場合、導体の表面、すなわち、x=0(y>0)とy=0(x>0)において ポテンシャルがゼロ、u=0に写されるハズだ。f(z) = iz2を考えてやるとよい。 そうすると 等ポテンシャル線: xy = Const. 電気力線: x2 - y2 = Const. と簡単に溶けてしまう! f(z) = z+a2z-1 はJoukowski変換と呼ばれ、流体力学におけるPotential問題への応用例である。 流体力学はちょっと分かんないのでf(z) = (z+a2z-1)iを考える。 z=reitと表すとu = (-r+a2/r) sin(t) v = (r+a2/r) cos(t)に写されることが分かる。 u=Const.の直線に写されるz空間における曲線を逆に考える。 まず簡単なのは u=0 とすると sin(t)=0 ⇔ t=0,π または -r+a2/r=0 ⇔ r=a u = -c ≠ 0 を考えると c = (r-a2/r) sin(t) ⇔ r-a2/r = c/sin(t) rについての二次方程式を解くとr = (1/2)[ c/sin(t) ± sqrt( (c/sin(t))2 +4a2 ) ]これは、θ→+0 の時 r→+∞、θ=π/2 の時 r=(1/2)(c±sqrt(c2+4a2))でaより大きい。 大体下図の感じ。c=0の線を考えるに、 半径a、原点Oの円の表面に上面には正電荷、下面には負電荷を帯電させた 時の等ポテンシャル面と見ることができる。そうするの先のrの式は 等ポテンシャル面の方程式である。 一次変換 一般の形は
f(z) = (az+b)/(cz+d)というもの。 今簡単にf(z) = (z-a)/(z+a)を考える。z-a = r1exp(it1) z+a = r2exp(it2)とするとω=f(z) = r1/r2 ei(t1-t2)zについて r1/r2 が一定だったとすると、ωに於いては原点を中心とし 半径をr1/r2とする円に写像されることが分かる。 では、r1/r2 が一定なzはどんな図形(おそらく曲線だろう)だろうか。 点z=aと点z=-aからのキョリの比が一定の点は実はある円の円周を描く。 これはアポロニウスの円と呼ばれ初等幾何で示される。 つまり、fによって円に写されるのは円なのだ。
11/17 r1/r2 < 1 なら右面の円で、r1/r2 > 1なら左面の円になる。 では、これを用いて静電ポテンシャル問題を解こう。 (r1, r2, a)で定まるアポロニウスの円を導体とする。 さてこの円はω' = (z-a)/(z+a)によって円に写りさらにω = -log(ω')によって円(R・log(it))は直線(-log(R)-it)になる。 // ω = u + iv として // u = -log(R) は定数であり、これがポテンシャルであった 具体的には ω = -log(ω') = -log[(z-a)/(z+a)] = -log[sqrt((x-a)2 + y2)] + log[sqrt((x+a)2 + y2)] ガンマ関数(Gamma function) ガンマ関数は階乗(factorial)の複素平面への拡張である。Γ(z) = ∫0∞e-ttz-1dt (;Re(z)>0)と定義する。 z = x + iy に対して |tz| = |tx・tiy| = |tx|に注意すると|Γ(z)|≤∫0∞e-t|tz-1|dt = ∫0∞e-ttx-1dtだから x>0 であればこの無限積分は収束してΓも収束 する。その為に「Re(z)>0」とした。 複素平面のRe>0の範囲でΓ(z)は正則である。 更に Re(z)>1 の時, 以下のような部分積分でΓ(z) = ∫0∞e-ttz-1dt = [-e-ttz-1]0∞ + (z-1)∫0∞e-ttz-2dt = 0 + (z-1)Γ(z-1) = (z-1)Γ(z-1)を得る。 z=1でのガンマの値は具体的にΓ(1) = ∫0∞e-tdt = 1と求まって、自然数nに対してΓ(n) = (n-1)Γ(n-1) = (n-1)(n-2)Γ(n-2) = ... = (n-1)!Γ(1) = (n-1)!として階乗になっている。Γ(z+1) = zΓ(z)これを用いることで、-1<Re(z)<0 の範囲での Γ(z)を定義することができる。つまり、Γ(z) = (1/z)Γ(z+1)として定めていけば良い。 さらに繰り返せば、実部が(-2, -1), (-3, -2), ... の 領域でのガンマ関数が定義できる。 そしてこの定義の方法は、Re z>0のΓ(z)の解析接続である。 「Re z = 0, -1, -2, ...」では定義していないが実際これは 以下のように留数が求まることから特異点である事がわかる。(z-0)Γ(z) = (z-0)(1/z)Γ(z+1)→Γ(1) = 1 (when z→0) thus, z=0 はガンマ関数の一位の極である。 (z-(-n))Γ(z) = (z+n)/z/(z+1)/.../(z+n)Γ(z+n+1)→1/(-n)/(-n+1)/.../(-1)Γ(1) = (-1)n/n! したがって一般にゼロ以下の整数の点では一位の極である。ちなみにΓ(1+1/2) = (1/2)Γ(1/2) Γ(2+1/2) = (3/2)(1/2)Γ(1/2) Γ(n+1/2) = ((2n-1)/2)((2n-3)/2)…(1/2)Γ(1/2) = (2n-1)!!/2n・Γ(1/2)Γ(1/2) = ∫0∞ e-tt-1/2dt // sqrt(t) = x とおく = ∫0∞ exp(-x2)/x・(2x・dx) = 2∫exp(-x2)dx = √π (1/2)! = sqrt(π)/2無限乗積表示 ガンマ関数を無限乗積表示することを考える。 出発点としてe-t = lim[n→∞] (1-t/n)nこれをΓ関数の定義式に代入Γ(z) = lim[n→∞] ∫0n (1-t/n)n tz-1dt ∫0n (1-t/n)n tz-1dt = [(1-t/n)n tz/z] + (1/z)∫(1-t/n)n-1 tz dt = (1/z)∫(1-t/n)n-1 tz dt = (1/z)[(1-t/n)n tz+1/(z+1)] + (n-1)/z/(z+1)/n ∫(1-t/n)n-2 tz+1 dt = ... = (n-1)!/nn-1 /z/(z+1)/.../(z+n) ∫tz+n-1 dt = n!nz /z/(z+1)/.../(z+n)よって、Γ(z) = lim[n→∞] n!・nz /z/(z+1)/…/(z+n) これでもう良いのに n/(z+n)→1 (when n→∞) を代入したΓ(z) = lim[n→∞] (n-1)! nz/z/(z+1)/…/(z+n-1)これをGaussの公式という。 さらに分母分子を(n-1)!で割るとΓ(z) = lim 1/z・1/(z+1)・1/(z/2+1)・1/(z/3+1)…1/(z/(n-1)+1)・nz = lim nz/z Π[m=1, n-1] (1+z/m)-1 ---(*)更にnz = [n/(n-1)・(n-1)/(n-2)・…・2/1]z = Π[m=1, n-1] {(m+1)/m}z = Π[m=1, n-1] (1+1/m)zを代入してΓ(z) = lim (1/z)Π[m=1, n-1] (1+1/m)z/(1+z/m) = (1/z) Π[m=1, ∞] (1+1/m)z/(1+z/m)これをEulerの公式という。 //こっちのがキレイだ。 この右辺からも z=0, -1, -2,.. が特異点であることが分かる(Πの中の分母が0になるようなmが存在する)。キレイ。 ココらへんに来ると「誰々の公式」とか言ったもん勝ちに なってくる。 1+1/2+1/3+…+1/n はn→∞で無限に発散するが、 1+1/2+1/3+...+1/n - log(n) はn→∞で実数で値を 定め、その値をEuler数γ=0.57くらいという。 // (1/x)の[1, n]での積分値と幅1のリーマン和との差っぽいnz = exp(z・log(n)) = exp(z(1+1/2+...+1/n))・exp(z(log(n)-1-1/2-...-1/n) = e-γz Π[m=1,∞]ez/mをEulerの公式の一つ前(*)に代入してΓ(z) = (1/z)e-γz Π[m=1,∞] exp(z/m)/(1+z/m)これの逆数を取った1/Γ(z) = ze-γz Π(1+z/m)e-z/mこれをWeierstrassの公式というが、右辺は解析関数で正則 である。ということはΓ(z)に零点は存在しない。 // Eulerもキレイだけどこっちももっとキレイだ! このワイヤーストラスを使うとΓ(z)・Γ(-z) = -1/z2 Π1/(1+z/m)/(1-z/m) = -1/z2・πz / sin(πz)またΓ(1-z) = -zΓ(-z) を使えばΓ(z)Γ(1-z) = π/ sin(πz)という性質を得る。 これを用いればΓ(1/2)が簡単に求まる。 ディガンマ関数 ディガンマだけどΨで表す。Ψ(z) ≡ d/dz(logΓ) = Γ'(z) / Γ(z)これにWeierstrassの公式Γ(z) = z-1e-γz Π[m=1,∞] exp(z/m) / (1+z/m)を用いるとΨ(z) = d/dz[ -log(z)-γz + ∑[m=1,∞] {z/m - log(1+z/m)} ] = -1/z-γ+∑{1/m - 1/(m+z)}ディガンマに1以上の自然数nを渡すと∑の中が打ち消し合ってΨ(n) = -1/n-γ+∑[m=1, n] 1/m = -γ + ∑[m=1, n-1] 1/mStirlingの公式(--の近似)Γ(x+1) = ∫0∞ e-t tx dtであったが、今xが非常に大きな場合を考えよよう。 被積分側では変数はtのみでxは定数なのだけど 「t = xτ」とおこう。つまり変数をτに変換する。Γ(x+1) = ∫0∞ exp(-xτ) (xτ)x (xdτ) = xx+1 ∫exp(-xτ) τx dτ = xx+1 ∫exp[-x(τ-log(τ))]dτeの右肩には大きな数とf(τ)を乗じたものが乗っている。 鞍点法が有効な形にしたわけである。 鞍点法とはすなわち、大きなxに対してf(τ)はそれが最小となる 点の近傍でのテイラー展開の二次くらいまでの近似式をf(τ)として 用いることで近似する方法である。f(τ) = τ - log(τ) f'(τ) = 1-1/τ 故にf'(τ) = 0 ⇔ τ = 1 であり、ここでfは最小値を取る。 τ~1 の周りで f(τ) ~ 1 + (1/2)(τ-1)2 + …この二次までの式を代入すればΓ(x+1) ~ xx+1 ∫0∞ e-x(1+1/2・(τ-1)2)dτ = xx+1 e-x sqrt[2π/x] + … ~ sqrt(2π) xx+1/2 e-xこの最後の式を大きな数xに就いての(x!)の近似式として用いられる のをよく見るよ。
コメ(0) | トラ(0)